Finite Element Research

My Ph.D. work ended in the discovery of a new class of finite element methods called DPG* methods, as well as in classifying a nebulous category of methods called discrete least-squares methods (DLS methods). In addition, I wrote software for high-order adaptive computer simulations and developed specific for methods structural, fluid, and wave mechanics problems.

Numerical Methods

Much of my PhD research, supervised by Leszek Demkowicz, was spent focusing on discontinuous Petrov-Galerkin finite element methods (DPG methods). In my early postdoctoral work, I focused in part on a non-standard approach to finite element analysis which was dubbed the "surrogate matrix methodology." During my subsequent academic positions, my interests grew to include stochastic optimization, scientific machine learning, numerical relativity, and turbulence modeling. The following summaries only pertain to my early contributions to the field of finite element analysis.

DPG* Methods

hp-adaptive mesh refinement with a DPG* method for Poisson's equation on the L-shaped domain. Left: The DPG* solution. (Colour scale represents solution values.) Right: The corresponding hp quadtree mesh delivered by an hp-adaptive algorithm after fifteen refinements. (Colours represent the polynomial degree p.)

DPG* methods are dual to DPG methods. In a well-defined sense, DPG, as a methodology, can be viewed as a practical means to solve overdetermined Petrov–Galerkin discretizations of boundary value problems. In a similar way, DPG* delivers a methodology for underdetermined discretizations.

Demkowicz, L., Gopalakrishnan, J., and Keith, B. (2020). The DPG-star method. Comput. Math. Appl. [preprint] [doi]

Surrogate Matrix Methods

Left: Distribution of computational cost in an IGA problem. Right: Distribution of computational cost with a related surrogate method. The difference in absolute solver time and accuracy of the solution were negligible.

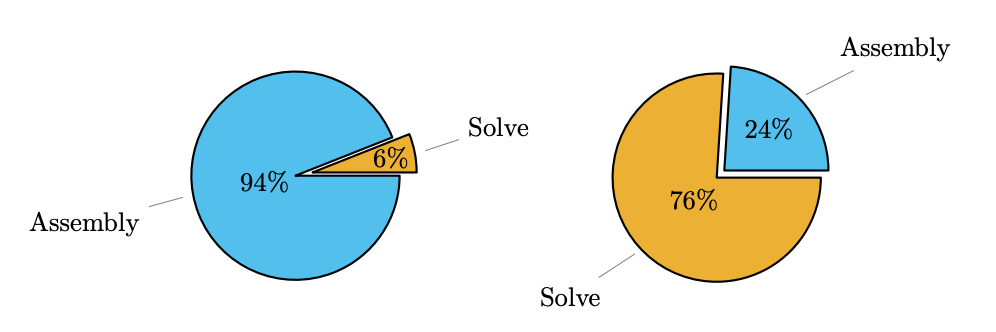
It can be shown that the majority of entries in the coefficient matrices generated by many Galerkin finite element methods can be computed by evaluating a small number of smooth so-called "stencil functions" at evenly-spaced points throughout the computational domain. Surrogate matrix methods provide low-cost coefficient matrices for such methods by simply evaluating approximations of these stencil functions. The methodology has been applied to classical finite element methods with lowest order simplicial elements as well as isogeometric methods, which employ high-order B-spline or NURBS bases.

In an ongoing series of papers, surrogate matrix methods have been successfully used in a large number of problems with steady or transient characteristics. This includes Poisson’s equation and p-Laplacian diffusion, membrane vibration, plate bending, Stokes’ flow, linear and nonlinear elasticity, and high frequency wave propagation problems. Using surrogate methods can significantly reduce the time to solution in isogeometric analysis (IGA) at a few million degrees of freedom or in large-scale matrix-free applications with billions of degrees of freedom. This ongoing work is part of Daniel Drzisga's PhD research.

Drzisga, D., Keith, B., and Wohlmuth, B. (2020). The surrogate matrix methodology: Accelerating isogeometric analysis of waves. Comput. Methods Appl. Mech. Engrg., 372:113322 [preprint] [doi]

Drzisga, D., Keith, B., and Wohlmuth, B. (2020). The surrogate matrix methodology: A reference implementation for low-cost assembly in isogeometric analysis. MethodsX 7:100813 [preprint] [doi] [code]

Drzisga, D., Keith, B., and Wohlmuth, B. (2020). The surrogate matrix methodology: Low-cost assembly for isogeometric analysis. Comput. Methods Appl. Mech. Engrg., 361:112776 [preprint] [doi]

Drzisga, D., Keith, B., and Wohlmuth, B. (2019). The surrogate matrix methodology: a priori error estimation. SIAM J. Sci. Comput., 41(6):A3806-A3838 [preprint] [doi]

DLS Methods

Left: Condition number growth of various stiffness matrices. Notice the O(h^-1) growth in green. This is comes from reformulating the assembly algorithm, not from a new preconditioner. Right: A study in robustness and sensitivity to round-off error with the frequency-domain acoustic wave equation near resonance. Here, the DLS solutions converge while the others diverge.

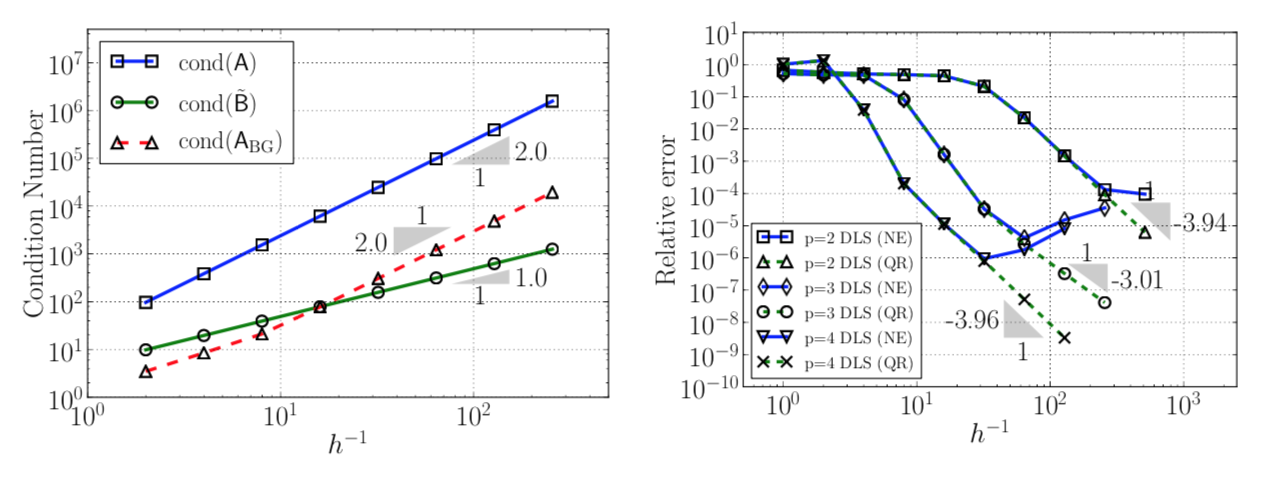
From extensive research on DPG methods, the term discrete least-squares finite element method (DLS method) was coined. The discrete linear systems in DLS methods have a very specific algebraic structure which can be exploited to accelerate computation or to reduce round-off error.

Keith, B., Petrides, S., Fuentes, F., and Demkowicz, L. (2017). Discrete least-squares finite element methods. Comput. Methods Appl. Mech. Engrg., 327:226-255. [preprint] [doi]

Goal-Oriented Methods

Far left: Manufactured solution with a large gradient in the region coloured deep red. Center left: A region of interest (shaded light red) where the solution is declared to be of primary interest. Center right: A goal-oriented adaptive mesh refinement pattern which seeks to minimize the numerical error in the region of interest. Far right: Vast improvement in the efficiency across three new goal-oriented refinement strategies, shown in red, green, and blue, in comparison to a standard adaptive mesh refinement strategy, shown in black.

Goal-oriented methods are tailored for accuracy in a specific output. With goal-oriented methods, great efficiency improvements can be achieved because a globally high-quality solution is often not necessary. Once the output is determined, there are many different ways in which to seek efficiency improvements. One way is through goal-oriented adaptive mesh refinement, which can be rigorously formulated in non-symmetric functional settings and applied to DPG methods.

Keith, B., Vaziri Astaneh, A., and Demkowicz, L. (2019). Goal-oriented adaptive mesh refinement for discontinuous Petrov–Galerkin methods. SIAM J. Numer. Anal., 57(4):1649-1676 [preprint] [doi]

Applications

Solids

Left: Adaptive mesh refinement with different formulations for a singular solution. Center: Schematic diagrams of a complicated sheathed hose problem. Right: The computed azimuthal stress on the two materials in the hose.

In a sequence of two papers, Federico Fuentes and I analyzed four different formulations — denoted strong, mixed, primal, and ultraweak, respectively (see figure; left) — of a common linearized elasticity model. This project culminated in the analysis of a very difficult high material contrast coupled rubber and steel model (see figure; center and right). Here, due to the incompressibility of the rubber, standard displacement-only methods will often break down or ''lock.'' Additionally, the steel in the model is very thin and so, likewise, some alternative formulations will often break down there. Our solution was to develop a special method coupling two different formulations together at the material interface; hence, greatly improving the accuracy possible solely with either individual formulation.

Fuentes, F., Keith, B., Demkowicz, L., and Le Tallec, P. (2017). Coupled variational formulations of linear elasticity and the DPG methodology. J. Comput. Phys., 348:715-731. [preprint] [doi]

Keith, B., Fuentes, F., and Demkowicz, L. (2016). The DPG methodology applied to different variational formulations of linear elasticity. Comput. Methods Appl. Mech. Engrg., 309:579-609. [preprint] [doi]

Fluids

Left: Velocity field and stress tensor component profiles from an Oldroyd-B fluid model. Center: Convergence through adaptive mesh refinements of the horizontal traction component of the solution. Right: An example of an adaptively refined mesh after five refinement steps.

Viscoelastic fluid models are commonly used in engineering to simulate blood and polymer melts. These models are well-known to very challenging both in simulation and in mathematical analysis.

I developed a new DPG finite element method of the Oldroyd-B viscoelastic fluid model which is intrinsically stable throughout a broad range of model parameters. I then studied parameter-dependent adaptive mesh refinement with the method. The simulations for this project were completed using the Camellia software library.

Keith, B., Knechtges, P., Roberts, N.V., Elgeti, S., Behr, M., and Demkowicz, L (2017). An ultraweak DPG method for viscoelastic fluids. J. Non-Newton. Fluid Mech., 247:107-122. [preprint] [doi]

Waves

Far left: A 2D computational domain with a perfectly matched layer (PML). Center left: A 3D computational domain with a PML. Center right: The x-component of the displacement from a 2D elastodynamics model. Far right: The x-component of the electric field from a 3D electromagnetics model.

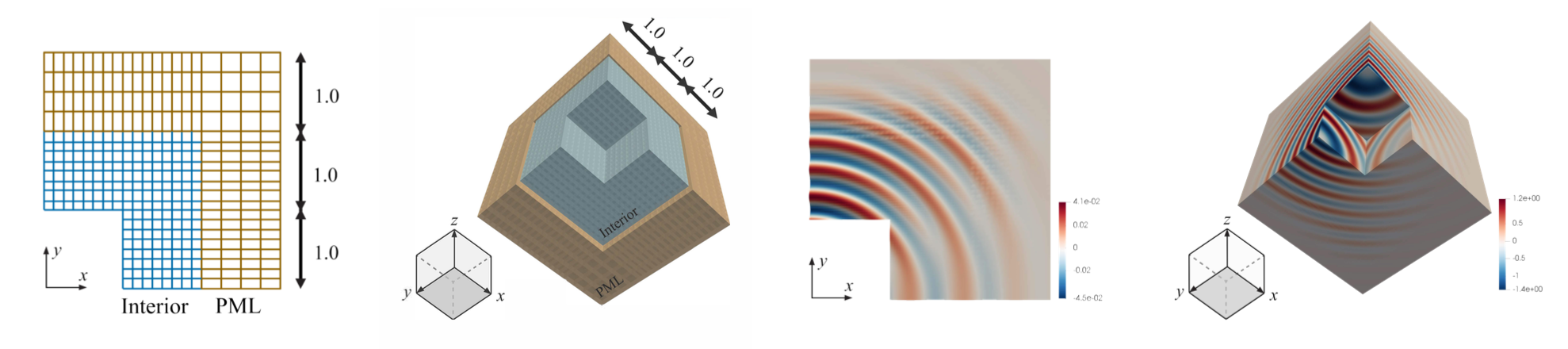
Perfectly matched layers (PMLs) are a very widespread type of artificial absorbing boundary layer used in numerical methods for wave propagation problems defined on unbounded domains. In order to lay the groundwork for some of my colleagues to begin their dissertation research, Ali Vaziri Astaneh and I developed PMLs for high-order DPG methods for acoustic, elastodynamic, and electromagnetic models.

Vaziri Astaneh, A., Keith, B., and Demkowicz, L. (2019). On perfectly matched layers for discontinuous Petrov–Galerkin methods. Comput. Mech., 63(6):1131-1145 [preprint] [doi]

Software

I have written a significant amount of software in Fortran, Matlab, Python, and C++. Some of the software projects which I have led or contributed to are described below.

hp2D/hp3D

Throughout my PhD studies, I maintained and contributed to hp2D and hp3D. These two finite element libraries, written in Fortran and developed by Leszek Demkowicz, have complete 2D/3D support for local hierarchical anisotropic h- and p-refinement with one level of hanging nodes and shape functions for all standard elements conforming in each of the canonical de Rahm complex of Hilbert spaces:

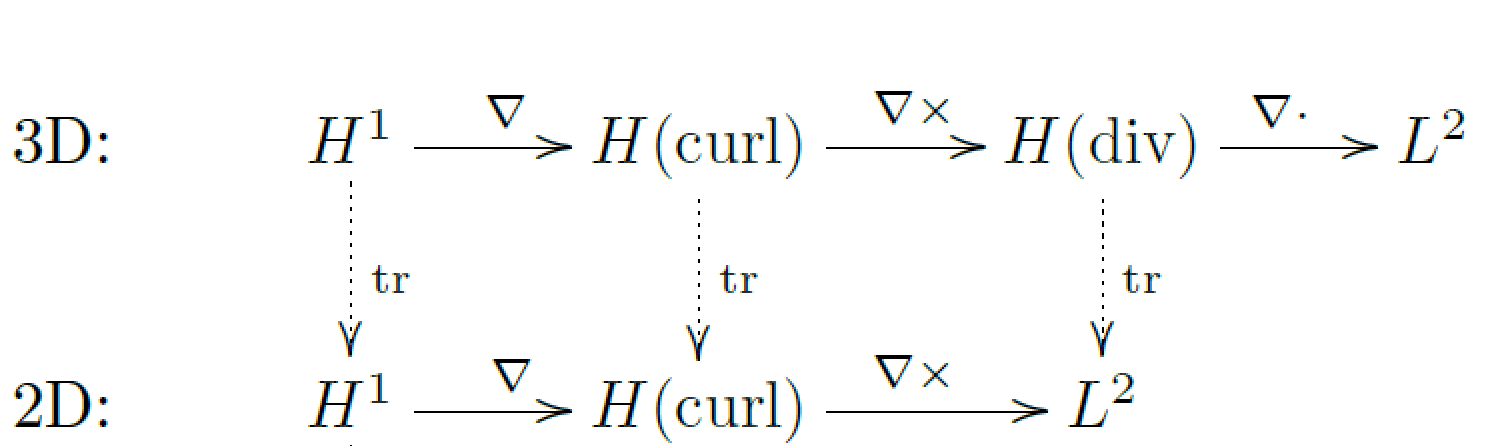
The software is not open-source due to limited documentation, but it is well-used by the Electromagnetics and Acoustics Group at the Oden Institute and by many of their collaborators.

ESEAS

Left: Illustrations of the 1D, 2D, and 3D elements supported by the ESEAS software. Right: Illustration of the novel shape function construction for pyramid elements.

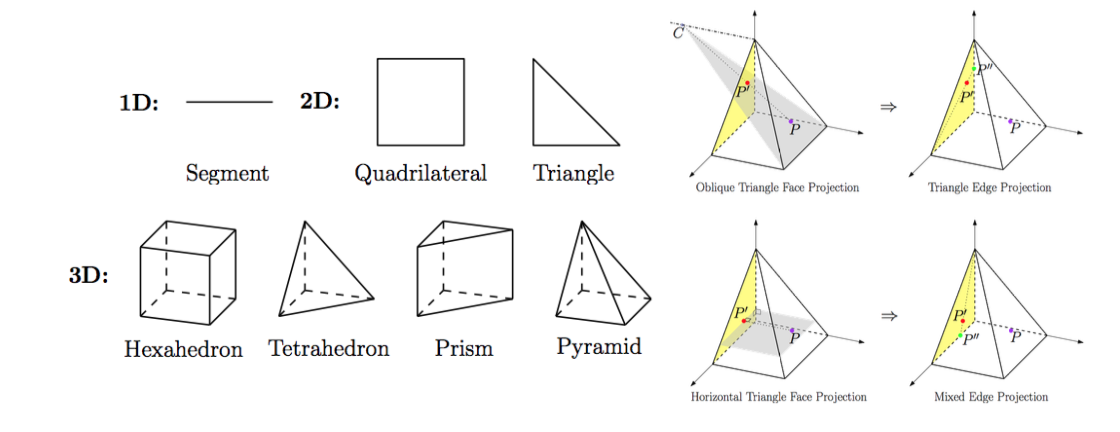
The ESEAS (exact sequence elements of all shapes) software library supports a complete set of features for evaluating shape functions in high-order finite element methods written in the Fortran 77 standard. The library is innovative for its support for all standard elements in one, two, and three spatial dimensions for arbitrary polynomial order (see figure above; left). It relies on a minimal set of hierarchical routines to construct all the shape functions. This hierarchical construction was the breakthrough which lead to the first explicit construction of arbitrary order pyramid elements (see figure above; right).

ESEAS is currently being used inside hp2D and hp3D, HOFEM, and Sierra. It is being rewritten and optimized in C++ for the Trilinos and MFEM libraries.

Fuentes, F., Keith, B., Demkowicz, L., and Nagaraj, S. (2015). Orientation embedded high order shape functions for the exact sequence elements of all shapes. Comput. Math. Appl., 70(4):353-458. [preprint] [doi] [code]

Camellia

The Camellia software library is a C++ toolbox developed by Nathan Roberts which uses Sandia's Trilinos library of packages. It is a publicly available software with many tools for rapid implementation of finite element methods including discontinuous Galerkin (DG), discontinuous Petrov-Galerkin (DPG), DPG*, hybridizable discontinuous Galerkin (HDG), and first-order system least-squares methods (FOSLS).

Download Camellia

Download the Camellia manual